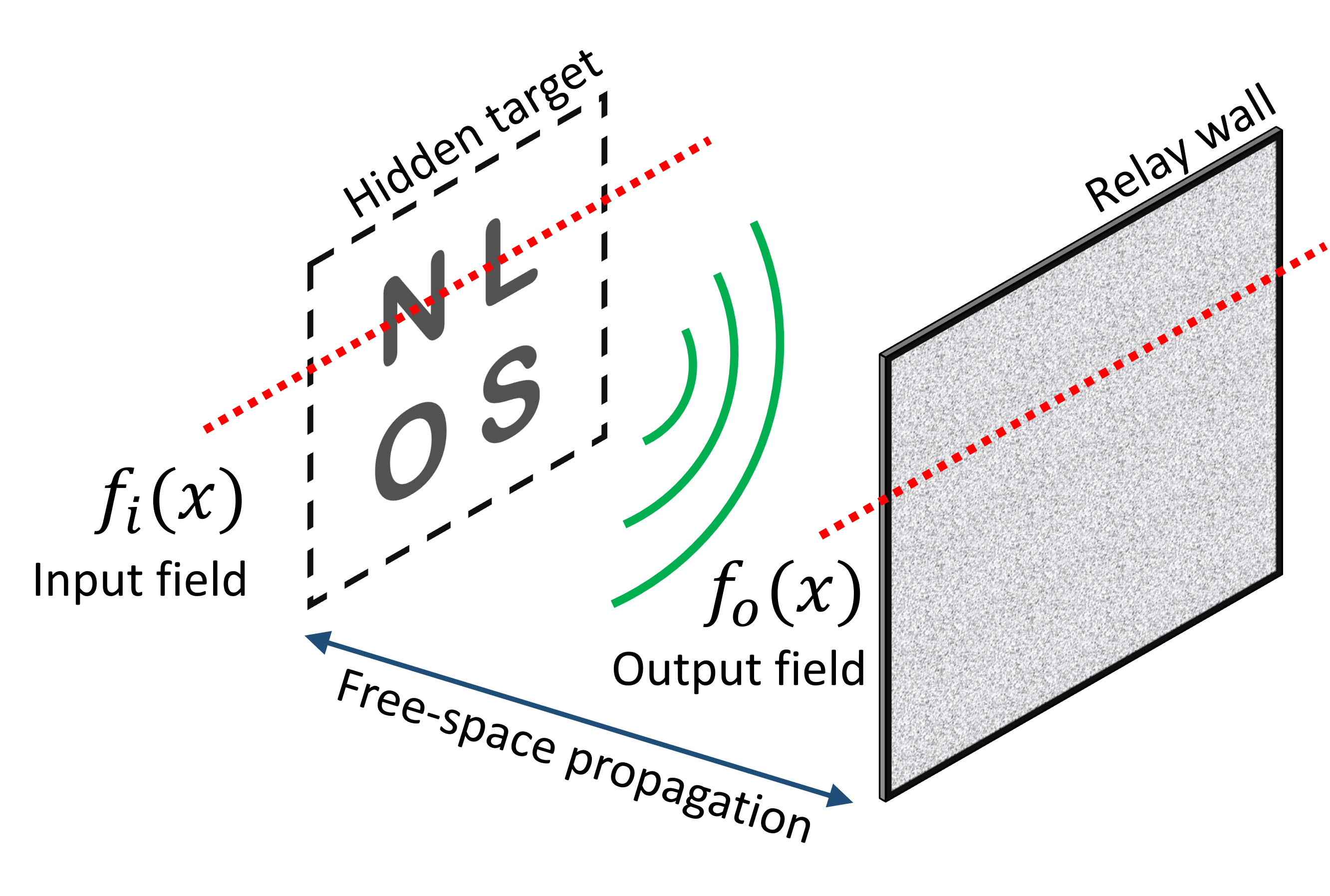
Non-Line-of-Sight imaging has been linked to wave diffraction by the recent phasor field method. In wave optics, the Wigner Distribution Function description for an optical imaging system is a powerful analytical tool for modeling the imaging process with geometrical transformations. In this paper, we focus on illustrating the relation between captured signals and hidden objects in the Wigner Distribution domain. The Wigner Distribution Function is usually used together with approximated diffraction propagators, which is fine for most imaging problems. However, these approximated diffraction propagators are not valid for Non-Line-of-Sight imaging scenarios. We show that the exact phasor field propagator (Rayleigh-Sommerfeld Diffraction) does not have a standard geometrical transformation, as compared to approximated diffraction propagators (Fresnel, Fraunhofer diffraction) that can be represented as shearing or rotation in the Wigner Distribution Function domain. Then, we explore differences between the exact and approximated solutions by characterizing errors made in different spatial positions and acquisition methods (confocal, non-confocal scanning). We derive a lateral resolution based on the exact phasor field propagator, which can be used as a reference for theoretical evaluations and comparisons. For targets that lie laterally outside a relay wall, the loss of resolution is geometrically illustrated in the context of the Wigner Distribution Function.

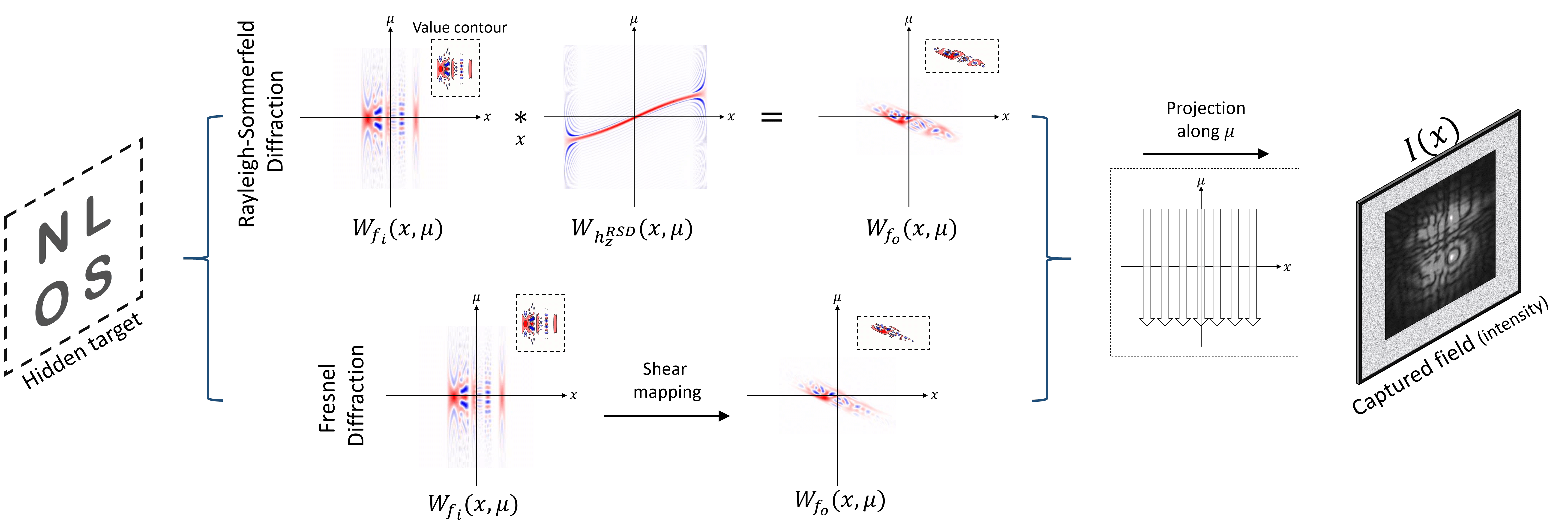Using Wigner Distribution Function to explain non-line-of-sight imaging. Captured temporal signals can be described as waves (Phasor field). This allows researchers to model Non-Line-of-Sight imaging problem as diffraction. Two main propagators (Rayleigh-Sommerfeld diffraction and the Fresnel diffraction) are shown to be useful for the Non-Line-of-Sight imaging. In this work, we have studied these two propagators in the Wigner Distribution Function domain.

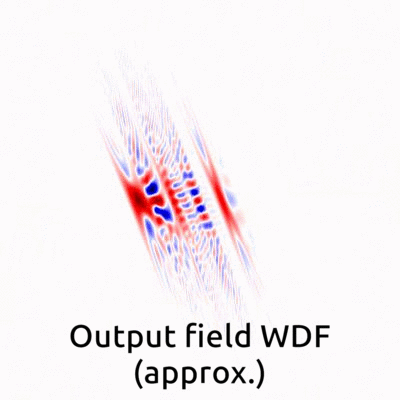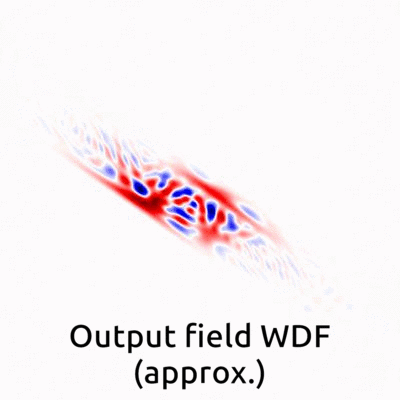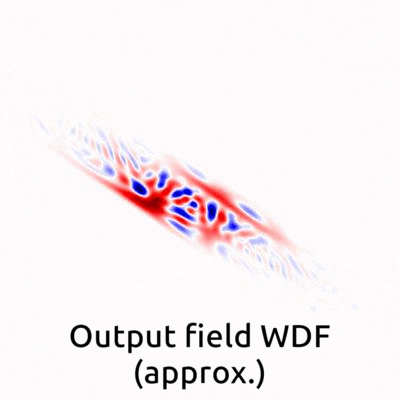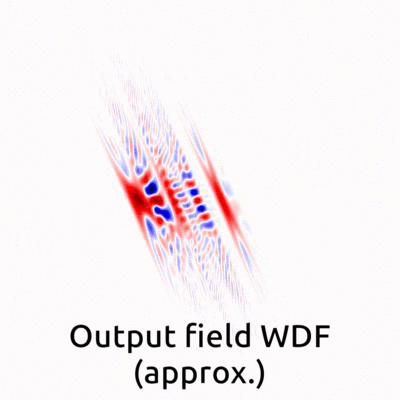
Geometrical interpretations in the Wigner Distribution Function domain. We found that the exact propagator (Rayleigh-Sommerfeld diffraction) and the approximated propagator (Fresnel diffraction) have different geometrical interpretations in the Wigner Distribution Function domain. In the Wigner Distribution Function domain, the approximated solution can be interpreted as a shearing process, whereas the exact does not have geometrical analytical close-formed expression.

Error between the exact and the approximated in the Wigner Distribution Function domain: Confocal measurements can be well-approximated by the Fresnel diffraction, which means that signals shear in the Wigner Distribution Function domain as distance. However, in the non-confocal situation, the exact solution is necessary.

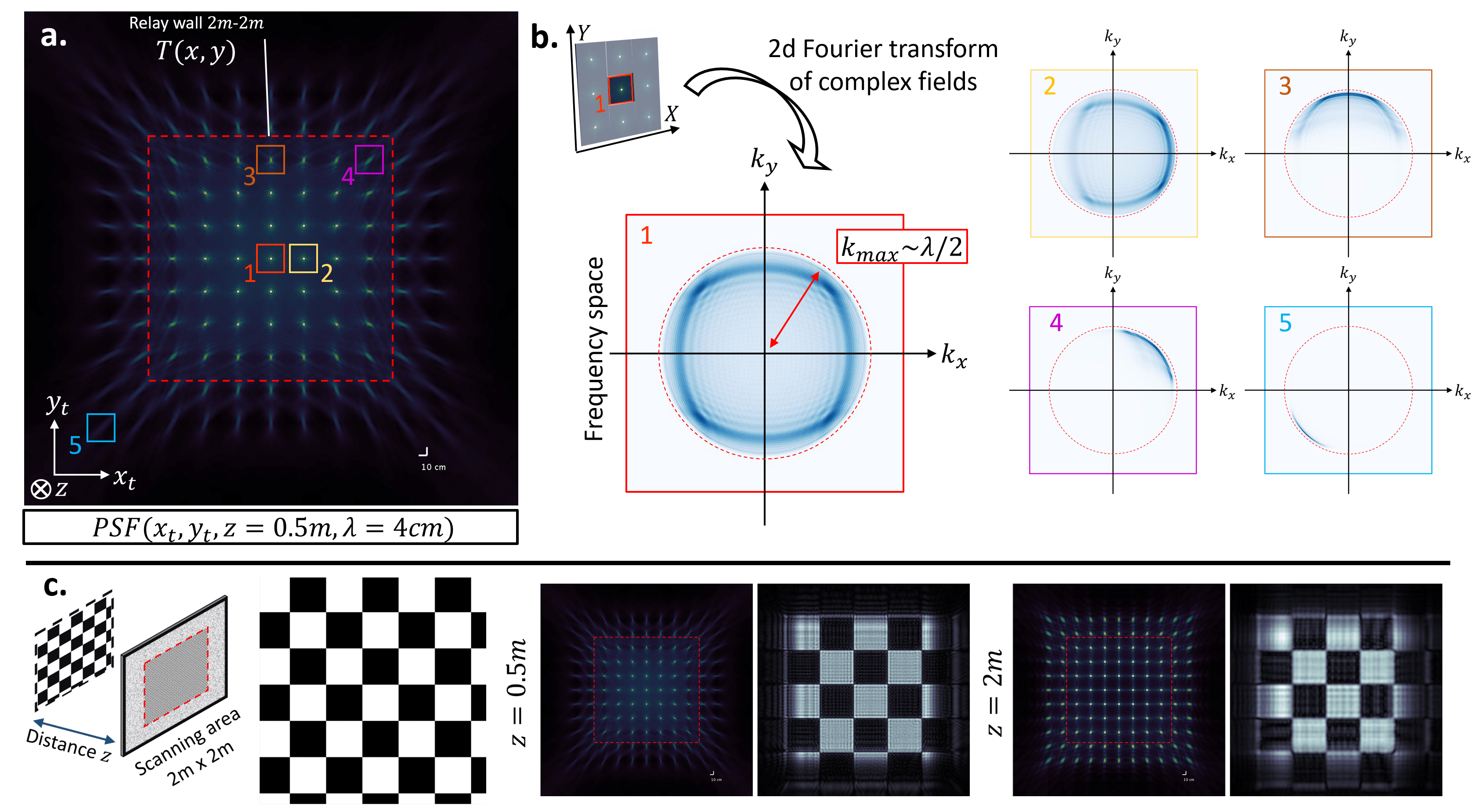Ideal reconstruction lateral resolution: With the exact diffraction model, we can characterize the best reconstruction quality by modeling resolution limits. Then we visualize this resolution limit as the point spread functions, field transfer functions as a function of relay wall size, spatial sampling space, central frequency, etc.

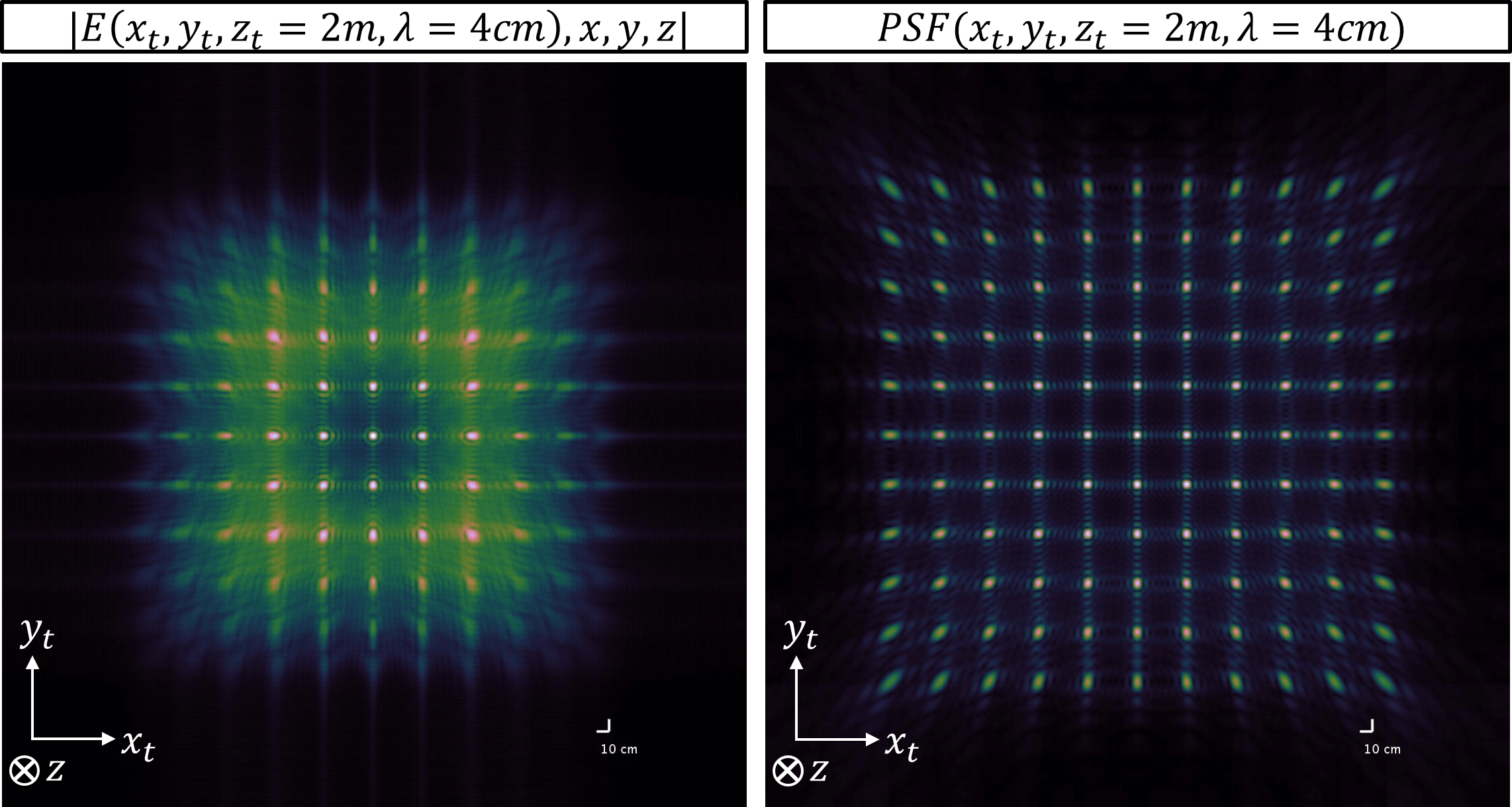Errors from the approximated propagator: Without too much surprise, the Fresnel diffraction is a reasonable approximation within the paraxial region. One has to aware of those errors considering acquisition methods, aperture size, central frequency as details are given in our paper.

Rethinking about sampling: Non-line-of-sight signals sampling on the relay wall can be described through an aperture function. To help better understand what is being used in practice, we show some examples like the loss of resolution as a relation to the scanning pattern on the relay wall.

We thank anonymous Reviewer 2 (Reviewer#5, ICCP2020) for valuable suggesting clarifications on Eq. (19) about resolution behaviors between confocal and non-confocal measurements. This work was funded by DARPA through the DARPA REVEAL project (HR0011-16-C-0025), the NASA NIAC program, and the AFOSR through the Young Investigator Program (FA9550-15-1-0208).